주기가 $T$ 인 연속함수 $f(t)$ 는 $f(t) = f(t - nT)$ 인 조건을 만족시킨다. $\,$ (단, n은 정수) 복소지 함수 $( complex expotional function)$ 의 직교성 $(orthogonality)$ 을 이용하면 임의의 주기함수를

$f(t)=\frac {1}{T} \sum_{n = -\infty}^{\infty} F_{n}e^\frac {i2\pi nt}{T} (11.1)$

과 같이 복소지함수의 선형결합으로 전개할 수 있는데, 이를 푸리에 급수 $(Fourier series)$ 라 한다.

$F_n$ 은

$F_{n} = \frac {1}{T} \int_0^T f(t)e^\frac {-i2\pi nt}{T} dt \qquad (11.2)$ 로 주어진다.

$F_0$ 는 함수 $f(t)$ 의 한 주기에 대한 평균값에 해당하며, $F_{n}$ (단, n => 1 ) 의 실수부와 허수부는 각각 $f(t)$의 주파수가 $n/T$ 인 우함수(코사인 함수) 성분과 기함수 (사인함수) 성분의 크기를 나타낸다.

$f(t)$ 가 실함수 $(real function)$ 일 때, 식 (11.1) 의 켤레복소수 $(complex conjugate)$ 를 취하고 $n \to -n$ 으로 바꾸면 $F_{n}=F_{-n}$ 임을 보일 수 있다. 즉, 실함수에 대해 $F_{n}$ 은 켤레대칭 $(conjugate symmetric)$ 이다. 이 경우,

오일러 공식 $(Euler’s formula)$

$e^{i\theta} = cos{\theta} + isin{\theta} \qquad (11.3)$ 를 이용하여 , 식 (11.1)을

$f(t) = a_{0} \quad + \quad \sum_{n = 1}^{\infty} a_{n}cos(\frac {2\pi nt}{T}) \quad + \quad \sum_{n = 1}^{\infty} b_{n}sin(\frac {2\pi nt}{T}) \qquad (11.4)$ 와 같이 사인함수와 코사인함수의 선형결합으로 전개할 수 있다.

여기서 $a_{0}=F_{0}$ 이고

$a_{n} = F_{n} + F_{-n} \quad b_{n} =i( F_{n} + F_{-n} ) \qquad (n \geq 1) (11.5)$ 이다.

따라서, $f(t)$ 가 우함수라면 $b_{n}=0$ $( 또는 F_{n} = F_{-n} )$ 을 만족시키고, 기함수라면 $a_{n}=0$ $(또는 F_{n} = - F_{-n})$ 을 만족시킨다.

파이썬의 $mpmath$ 라이브러리는 복소수연산이 가능하며 $mpmath.fourier()$ 함수는 푸리에 급수의 계수를 계산한다.

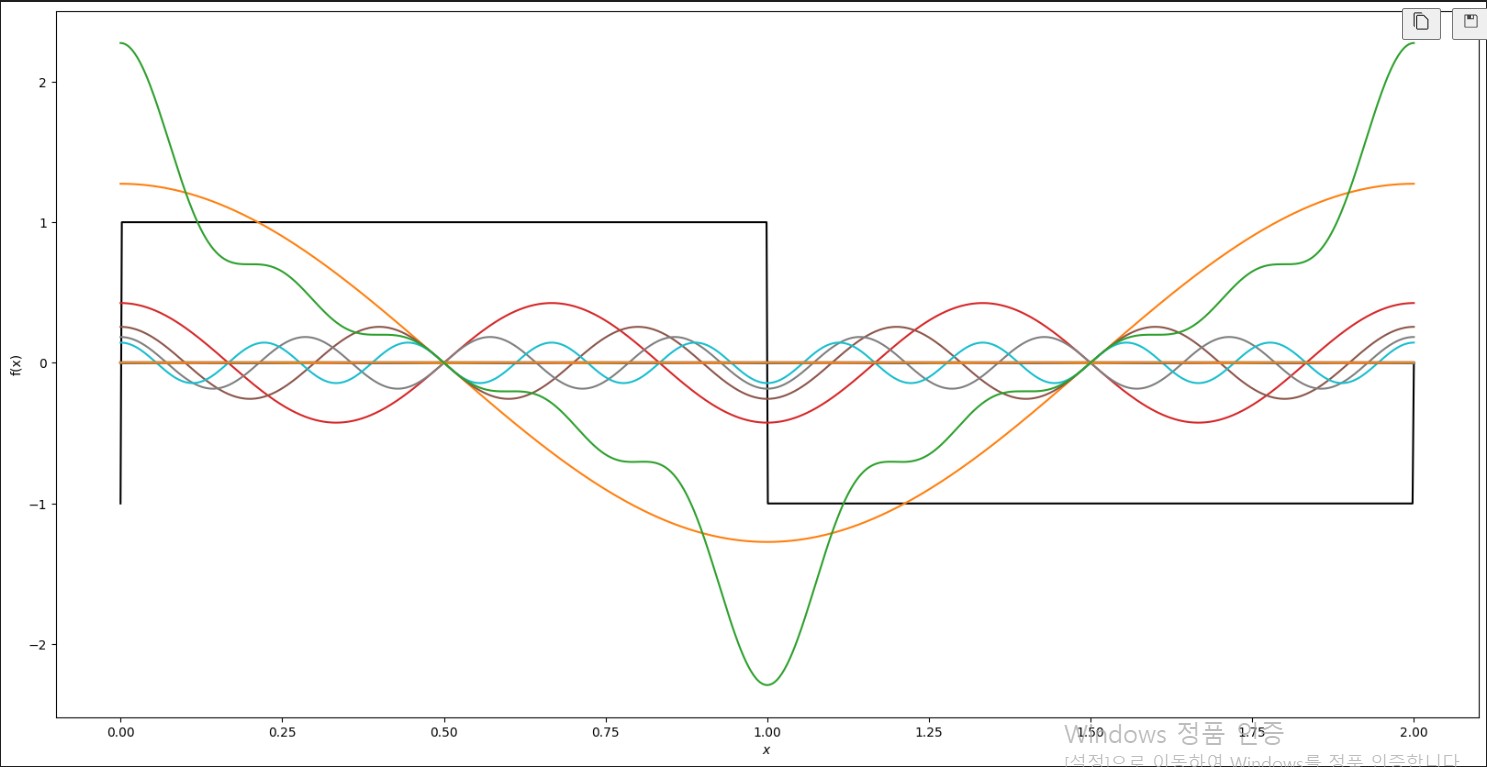
1. 주기가 $T=2$ 인 사각파 $f(t)= 1\quad(0 \leq t \leq 1),-1\quad(1 < t \leq 2)$

의 푸리에 급수를 구하고 그래프를 확인하시오. 이문제의 해는

$f(t) = \, \frac {4}{\pi} \sum_{n=1,3,5,…}^\infty n^{-1}sin(\frac {2\pi n t}{T})$ 다.

(풀이)

$a_{0}=\frac {1}{l} \int_0^1 dx + \frac {1}{l} \int_1^2 -dx = 0$

$a_n = \int_0^1 cos{n\pi x} dx - \int_1^2 cos{n\pi x} dx = \frac {1}{n\pi} (sin{n\pi x} - 0 - sin{2n\pi} + sin{n\pi x}) = 0$

$b_n = \int_0^1 sin{n\pi x} dx - \int_1^2 sin{n\pi x} dx = \frac {1}{n\pi}(cos{n\pi x} - 1 - cos2n\pi + cos{n\pi x})$

$if$

$n = even, 0$

$n = odd, \frac {-4}{n\pi}$

$f(x) = \frac {4}{\pi} \sum_{n=1,3,5,…}^\infty n^{-1}sin({2\pi n t})$

$python$을 이용하여 $matplotlib$ 으로 급수 표현하기

from mpmath import mp
import numpy as np
import matplotlib.pyplot as plt


def function(t):
    if 0 < t < 1:
        return 1
    elif t < 2:
        return -1
    else:
        return 0
    

N,T = 10, 2 


c,s = mp.fourier(function,[0,T],N)

num = 1000
t = np.linspace(0,T,num)


a_n = np.array(c)[:,np.newaxis]
b_n = np.array(s)[:,np.newaxis]
print(a_n)
print(b_n)


n = np.arange(N+1)[:,np.newaxis]

cos = a_n*np.cos(2*np.pi*n*t/T)
sin = b_n*np.cos(2*np.pi*n*t/T)


f = np.zeros(num)
for i in range(num):
    f[i] = function(t[i])


fig = plt.figure(1,figsize = (20,10))
plt.plot(t,f,'b')
plt.plot(t,sin.T)
plt.plot(t,cos.T)
plt.plot(t,sum(sin + cos))
plt.xlabel(r'$x$')
plt.ylabel(r"f(x)")
plt.show()